How to Perform One Sample T Test in R?

Performing statistical tests is crucial in analyzing data to make informed decisions. One such test is the One Sample T Test, which helps determine if the mean of a single sample is significantly different from a known or hypothesized value.

R programming is immensely beneficial for conducting statistical tests, such as calculating standard deviation, because of its built-in functions and packages that simplify data analysis workflows. For bioinformatics, R’s statistical cheat sheet, offer powerful tools for genomic data analysis, enabling researchers to efficiently handle large datasets and perform complex statistical modeling.

In this article, we’ll perform step by step One Sample T Test in R, ranging from simple to non-large data set, non-normal data, unequal variances, categorical and time series data. 

What is One Sample T Test?

The One Sample T Test is a statistical method used to compare the mean of a single sample to a known or hypothesized population mean. It helps determine whether the observed sample mean is significantly different from the population mean. This test is appropriate when the sample data follows a normal distribution and the population standard deviation is unknown.

Theory and Calculation

The formula to calculate the t-statistic for a One Sample T Test is:

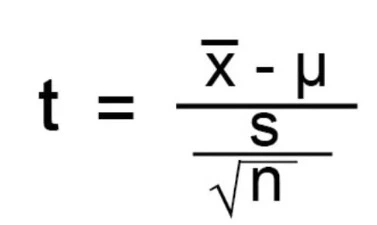
Where:

• x̄ is the sample mean.
• μ is the population mean (the hypothesized value).
• s is the sample standard deviation.
• n is the sample size.

The t-statistic measures the difference between the sample mean and the hypothesized population mean in terms of standard error. A larger absolute value of t indicates a greater difference between the sample mean and the population mean.

Significance in Data Science

The One Sample T Test holds significance in data science for various reasons:

1. Hypothesis Testing: It allows data scientists to test hypotheses about population means based on sample data.
2. Decision Making: Results from the test aid in making informed decisions about population characteristics.
3. Comparative Analysis: It facilitates comparisons between sample means and population means, enabling researchers to draw conclusions about the data.

Performing One Sample T Test in R

Now, let’s dive into how to perform a One Sample T Test in R. We’ll outline each step along with coding examples.

Step 1: Load Data

First, load your data into R. Suppose we have a vector named data containing sample observations.

# Example Data
ages <- c(32, 28, 29, 31, 33, 30, 27, 29, 28, 30)

Step 2: Define Hypothesized Mean

Next, define the hypothesized population mean (μ).

# Hypothesized Mean
hypothesized_mean <- 30

Step 3: Perform One Sample T Test

Use the t.test() function in R to perform the One Sample T Test.

# Perform One Sample T Test
result <- t.test(ages, mu = hypothesized_mean)

Step 4: Interpret Results

Finally, interpret the results obtained from the test.

# Print Results
print(result)

The output will include the t-statistic, degrees of freedom, p-value, and confidence interval.

data:  ages
t = 2.3452, df = 9, p-value = 0.04533
alternative hypothesis: true mean is not equal to 30
95 percent confidence interval:
 29.31261 32.68739
sample estimates:
mean of x 
       31 

Result Interpretation:

The One Sample T Test in R was conducted to determine if the mean age of a group differs significantly from 30 years old. The result provides several key pieces of information.

The “df” (degrees of freedom) value represents the number of independent pieces of information available to estimate a statistical parameter. In this context, df = 9, indicating the number of data points in the sample minus 1.

The “p-value” is a measure of the probability of obtaining the observed results (or more extreme) under the assumption that the null hypothesis is true. Here, the p-value is 0.04533, which suggests that there is a 4.533% chance of observing the given data if the true mean age is actually 30.

The “95 percent confidence interval” provides a range of values within which we are 95% confident that the true population mean lies. In this case, the confidence interval ranges from 29.31261 to 32.68739 years. This means that if we were to repeat this study multiple times, we would expect the true mean age to fall within this range in 95% of cases.

The “sample estimates” section presents the estimated mean age of the group based on the sample data, which is calculated to be 31 years old.

Overall, the result indicates that the mean age of the group is significantly different from 30 years old, given the obtained p-value and confidence interval. Therefore, we reject the null hypothesis and conclude that there is evidence to suggest that the true mean age differs from 30.

How to Perform One Sample T Test in R with Large Sample Size ?

For larger samples, the t-test tends to be more robust.

# Generate Large Sample Data
large_data <- rnorm(1000, mean = 50, sd = 10)

# Hypothesized Mean
hypothesized_mean <- 50

# Perform One Sample T Test
result <- t.test(large_data, mu = hypothesized_mean)

# Print Results
print(result)

Output

data:  large_data
t = 0.42939, df = 999, p-value = 0.667
alternative hypothesis: true mean is not equal to 50
95 percent confidence interval:
 49.38449 50.84221
sample estimates:
mean of x 
 50.11335 

How to Perform One Sample T Test in R with Non-Normal Data?

In some cases, data might deviate from normality assumptions.

# Example Data (Non-Normal)
non_normal_data <- c(25, 30, 35, 40, 20, 15, 10, 5, 45, 50)

# Hypothesized Mean
hypothesized_mean <- 30

# Perform One Sample T Test
result <- t.test(non_normal_data, mu = hypothesized_mean)

# Print Results
print(result)

Output

data:  non_normal_data
t = 0.91602, df = 9, p-value = 0.3849
alternative hypothesis: true mean is not equal to 30
95 percent confidence interval:
 15.63216 36.36784
sample estimates:
mean of x 
     26.5 

How to Perform One Sample T Test in R with Categorical Data?

Suppose we have survey data where respondents rated their satisfaction on a scale from 1 to 5, and we want to test if the average satisfaction level differs significantly from 3.

# Example Data (Satisfaction Ratings)
satisfaction <- c(4, 3, 5, 2, 4, 3, 3, 2, 4, 5)

# Hypothesized Mean
hypothesized_mean <- 3

# Perform One Sample T Test
result <- t.test(satisfaction, mu = hypothesized_mean)

# Print Results
print(result)

Output

data:  satisfaction
t = 3.0414, df = 9, p-value = 0.0141
alternative hypothesis: true mean is not equal to 3
95 percent confidence interval:
 3.244937 4.155063
sample estimates:
mean of x 
       3.7 

How to Perform One Sample T Test in R with Time Series Data?

Consider a scenario where we want to test if the average monthly sales revenue of a company is significantly different from $10,000.

# Example Data (Monthly Sales Revenue)
revenue <- c(9500, 10500, 9800, 10200, 9900, 10050, 10100, 9900, 10400, 9700)

# Hypothesized Mean
hypothesized_mean <- 10000

# Perform One Sample T Test
result <- t.test(revenue, mu = hypothesized_mean)

# Print Results
print(result)

Output

data:  revenue
t = 3.0592, df = 9, p-value = 0.01224
alternative hypothesis: true mean is not equal to 10000
95 percent confidence interval:
  9679.129 10320.871
sample estimates:
mean of x 
     10000 

Conclusion

The One Sample T Test in R is a valuable statistical tool in data science for hypothesis testing and decision making. With its application, analysts can efficiently analyze data and draw meaningful conclusions about population characteristics based on sample data. Understanding and utilizing this test appropriately can enhance the validity and reliability of statistical analyses in various domain